Principal Investigator:
Kong Research Group (KRG) is led by Dr. Jude Dzevela Kong, the founding Director of the Africa-Canada Artificial Intelligence and Data Innovation Consortium (ACADIC), the Executive Director of the Global South Artificial Intelligence for Pandemic and Epidermic Preparedness and Response Network (AI4PEP), and also the Executive director of Resilience Research Atlantic Alliance on Sustainability, Supporting Recovery and Renewal (Reasure2).
Objective of our research Program:
The long-term objective of our research program is to design novel mathematical, artificial intelligence and statistical models for decision makers in industry and government in order to provide important insights into local and global-scale socio-ecological challenges.
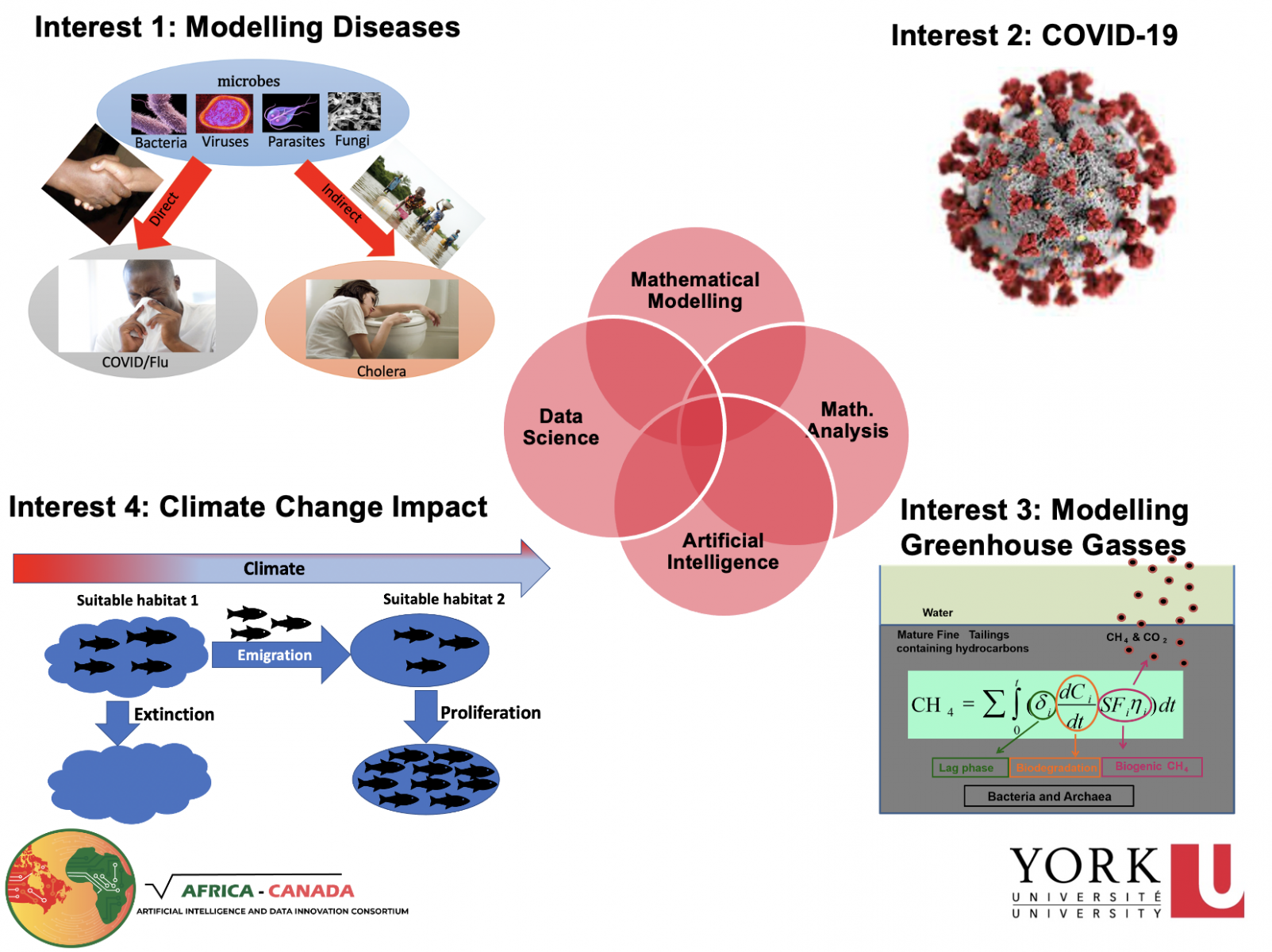
The short-term objectives include updating and designing new mathematical, artificial intelligence and statistical models that can predict, manage and forecast:
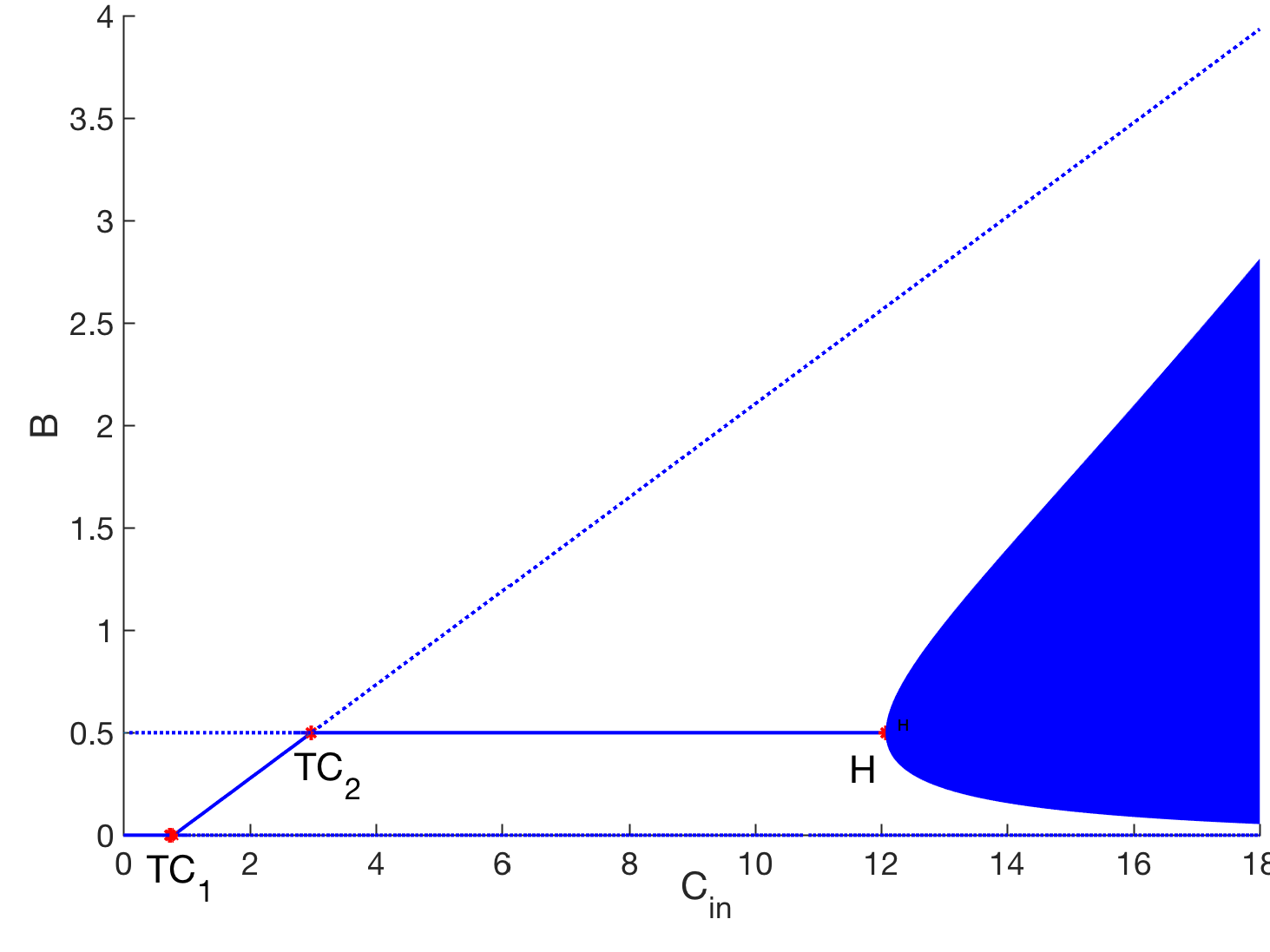
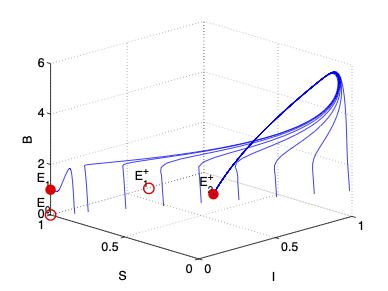
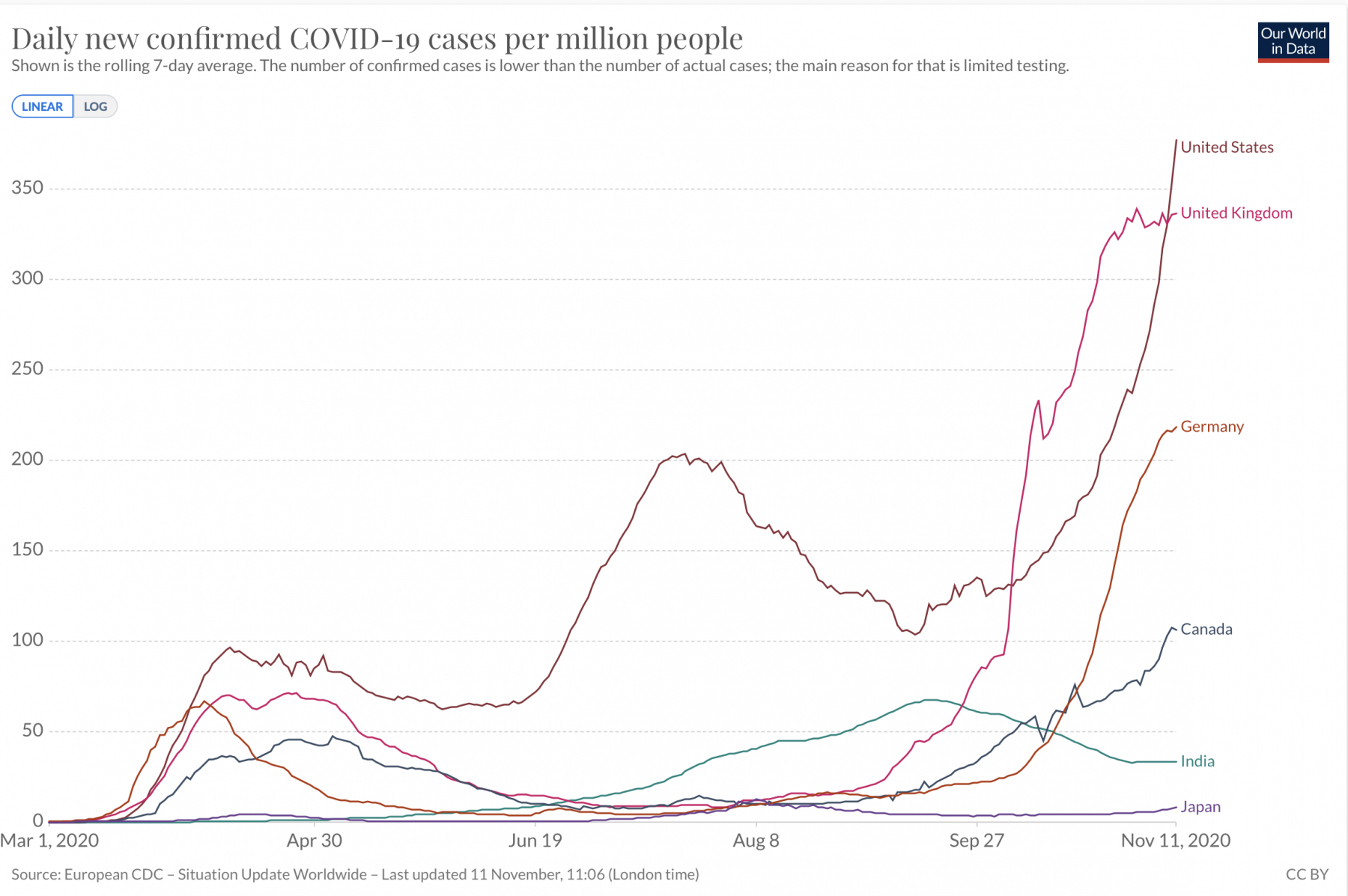
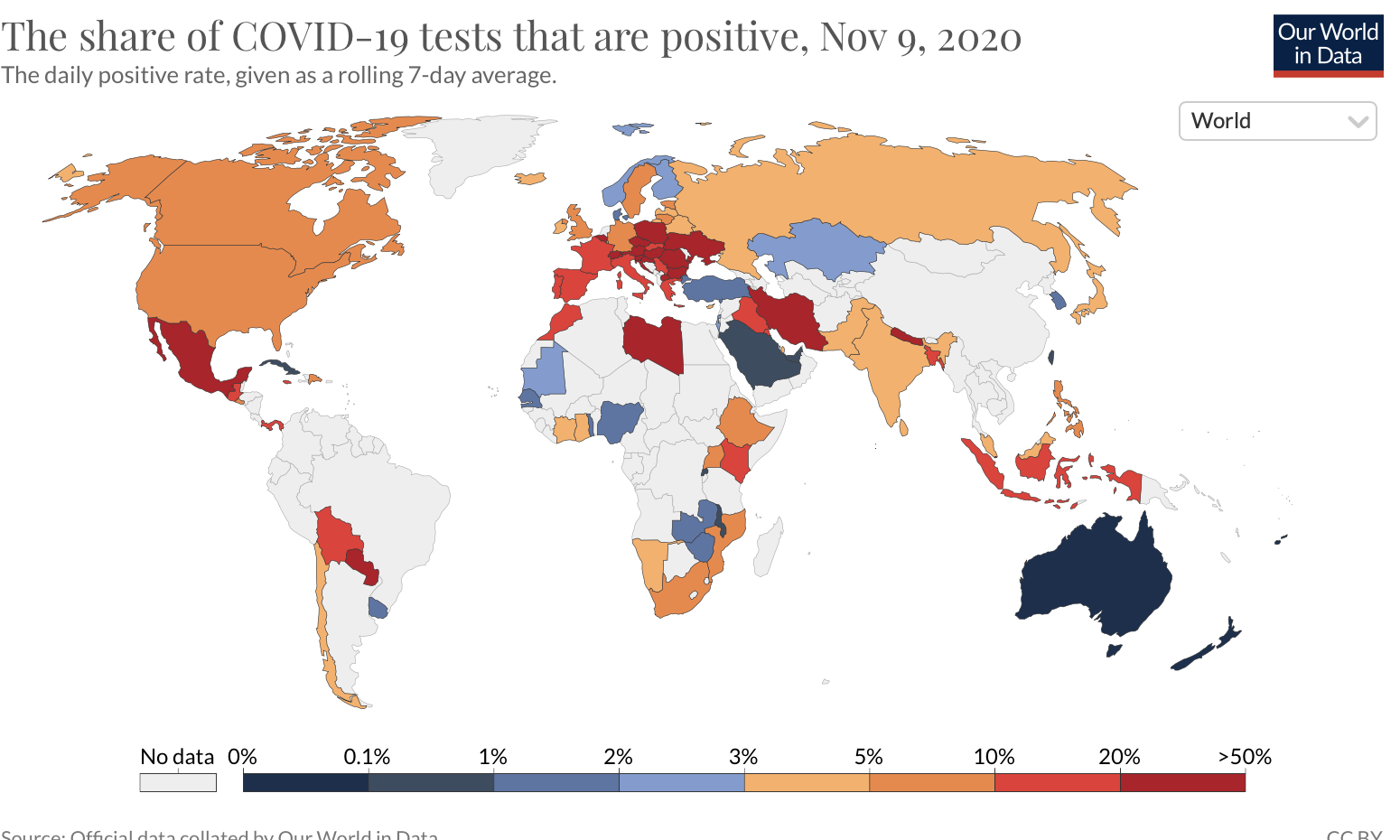
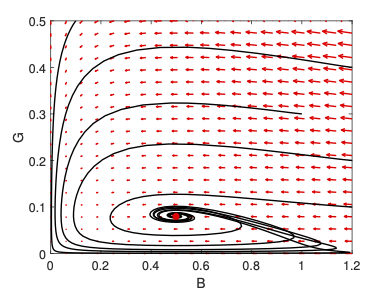
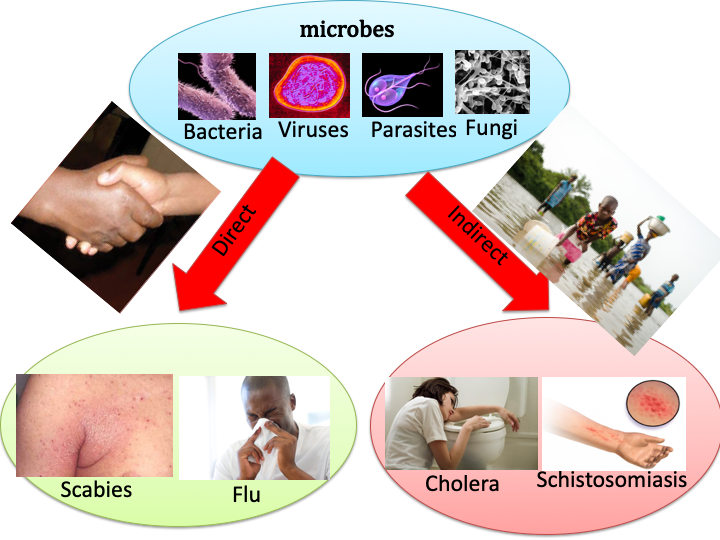
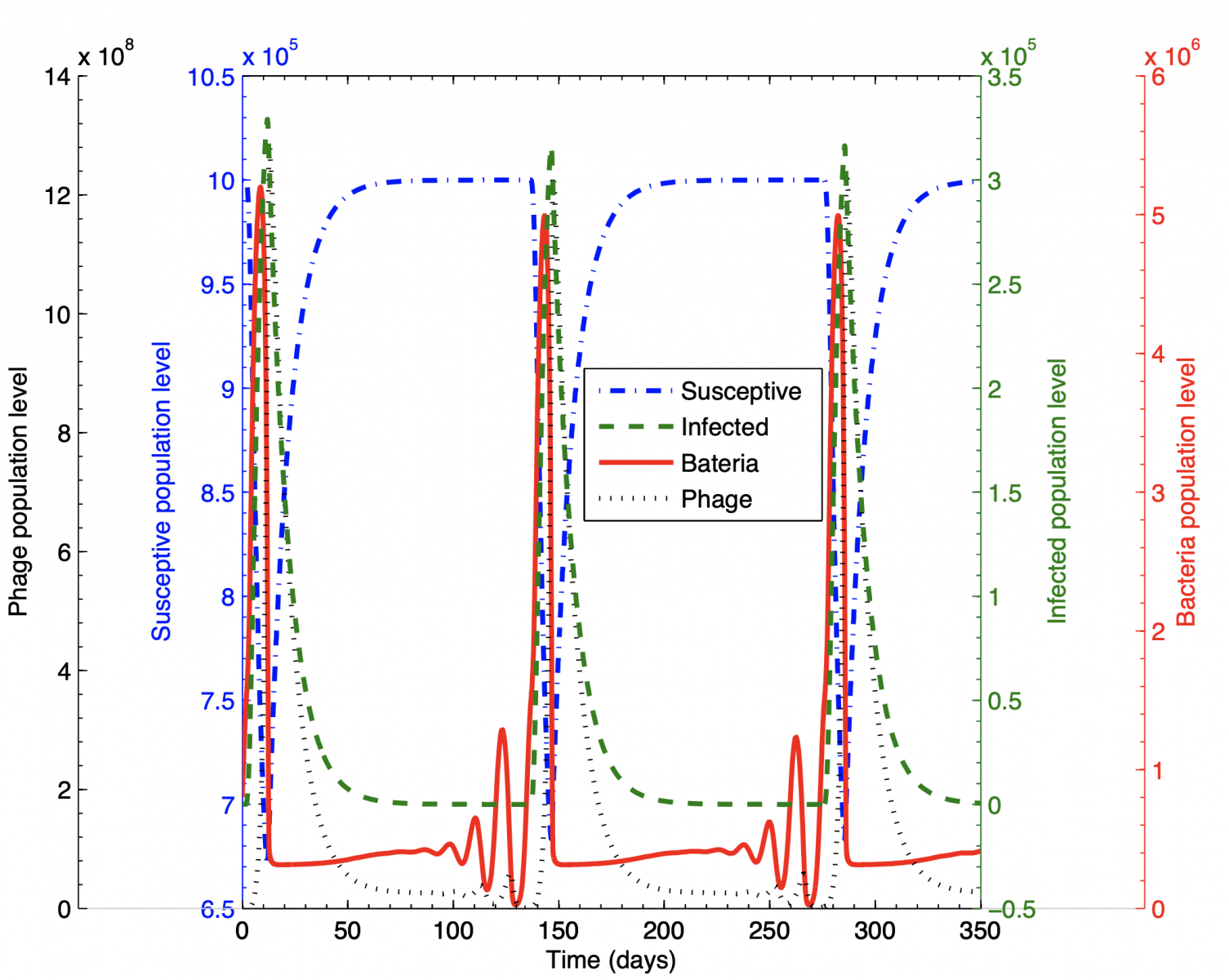
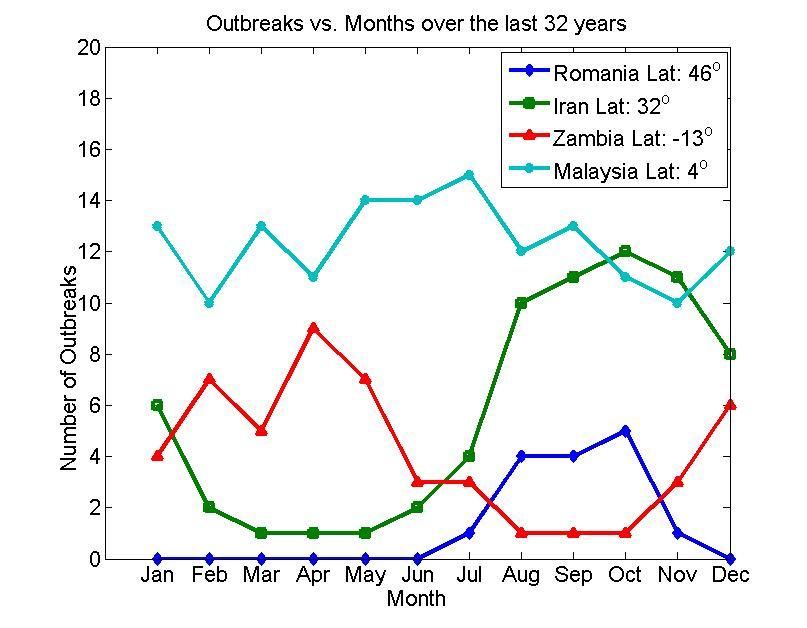
- The spread of infectious diseases
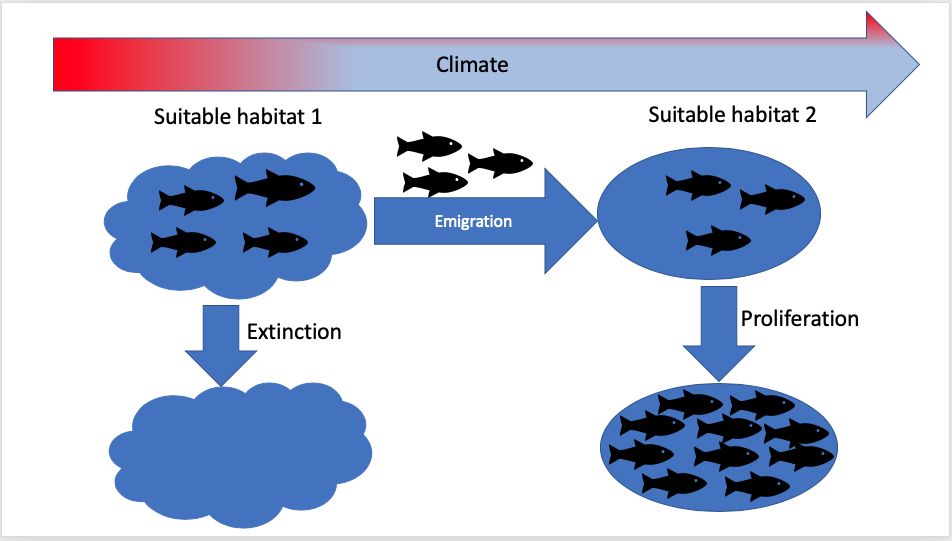
- Species (e.g fish) distribution under potential future ecosystem conditions (e.g climatic conditions);
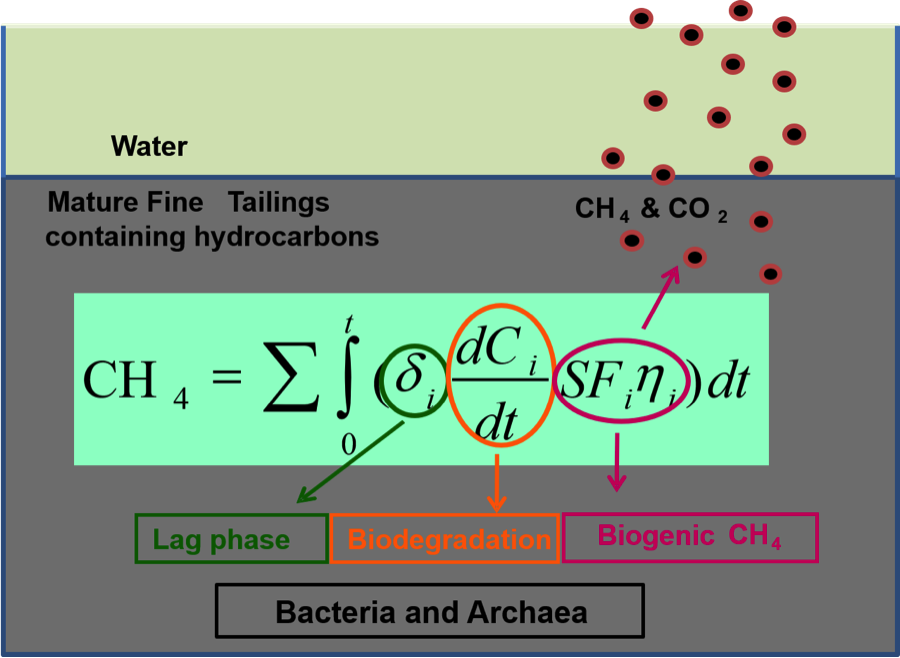
- Greenhouse gas emission from oil sand tailings; and
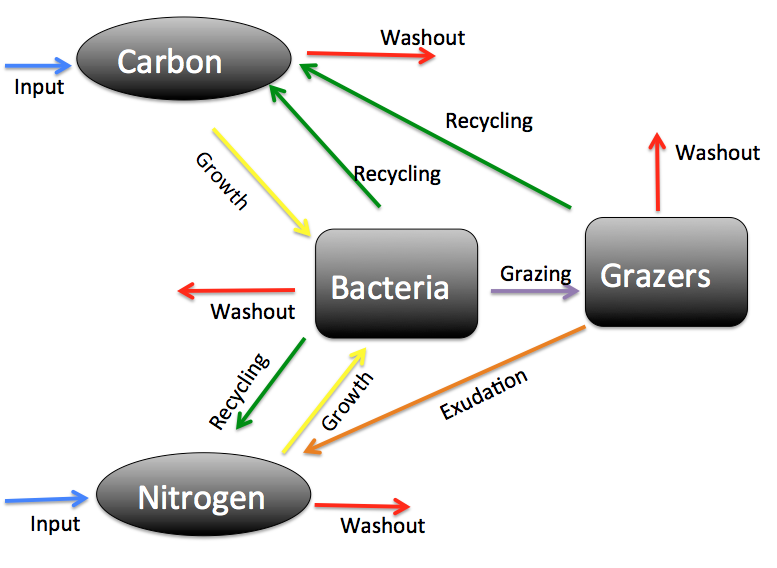
- Harmful algae blooms.
Expertise:
Dr. Jude Kong has a substantial track record in mathematical biology, infectious disease modelling, mathematical and statistical modelling, data science, artificial intelligence, citizen science, and participatory research as well as working with policy makers in government and industry.
Most of our postdocs, grad and undergrad students have backgrounds in mathematical biology, infectious disease modelling, applied mathematics, artificial intelligence, data science, public health, ecology, biological sciences, epidemiology, engineering etc
We train our postdocs, grad students and undergrad students to be experts in artificial intelligence, data science, mathematical and statistical modelling, computational modelling , data management, working with policy makers. Most of HPQS easily find jobs in the industry, governments, and academia.
Join us
We are actively looking for passionate undergraduate and graduate students, and postdocs to join our group. If our scientific interests overlap, and you will like to join us, please contact us before you apply so that we can discuss your application. In your email, please include a description of your interests and how they fit into our lab along with a CV, and unofficial transcripts. All students are welcome here regardless of race, religion, gender identification, sexual orientation, age, or disability status.
Events